Defining Clusters the Data-Driven Way
Why you shouldn’t use sector-based clusters to diversify your portfolio
Written by Sabr Research · April 2025
The illusion of Diversification through Sectors
Most investors and portfolio managers are familiar with the idea of diversification across sectors. The logic is simple: by holding stocks from different industries—technology, healthcare, energy, financials, and so on—you reduce your portfolio's overall risk. This sectoral classification is often based on static taxonomies such as the GICS (Global Industry Classification Standard), which assigns each company to a predefined category based on its primary business activity. However, these classifications can be misleading when it comes to actual market behavior—especially during periods of stress. During sharp market selloffs, correlations between seemingly unrelated sectors tend to spike, revealing hidden dependencies. Some ETFs classified under different sectors exhibit strikingly similar behavior during these crises, contradicting the promised benefits of diversification. A "diversified" portfolio may, in practice, be much more concentrated in risk than it appears on paper. This raises a fundamental question: Should we really trust these static sector definitions? Or is there a better way to define sectors based on how stocks actually move together?
A Data-Driven Alternative: Correlation Clusters
At Sabr Research, we believe that true diversification starts with understanding how assets behave, not how they're labeled. Instead of relying on preassigned sectors, we propose a data-driven approach to uncover the underlying structures in the market. The idea is to identify empirical sectors—clusters of stocks that truly move together—using their return correlations. This approach leverages unsupervised learning algorithms like k-means clustering and dimensionality reduction techniques such as t-SNE to analyze return data and visualize the real interconnections in the market. Let’s walk through how we built this analysis.
The Data
We begin with end-of-day prices of all S&P 500 constituents, from these raw prices, we compute the daily log returns defined as:- n is the number of stocks (rows).
- T is the number of trading days (columns): the last column correspond to the most recent observation and the first column to the latest.
Computing Correlation Distances
To build clusters of similarly behaving stocks, we use a distance metric based on correlation. For two stocks and , represented by their return series and , we define:- When two time series are perfectly correlated d=0.
- When uncorrelated d=1
- When perfectly anti-correlated d=2
Clustering with K-Means: Finding Empirical Sectors
Once we’ve computed the pairwise correlation distances between stocks, we want to group together those that move similarly. For this, we turn to k-means clustering, a widely used unsupervised learning algorithm that partitions a dataset into k clusters by minimizing intra-cluster dissimilarity:Making It Dynamic: A Weighted Version of K-Means
Markets evolve. A stock that used to behave like a utility may now trade more like a tech company. Regime shifts, earnings surprises, macro news, and structural changes can drastically alter the correlation structure over time. Yet classical clustering treats all data points equally, regardless of how old they are. To address this, we implemented a weighted version of k-means, where more recent observations have a larger influence on both the correlation distance and the cluster updates.Exponential Weighting Scheme
Let be a time series of daily log returns for a given stock. We define a set of weights , where more recent timestamps (i.e. larger t) get higher weights. The weighting scheme is defined as:- Weighted mean:
- Weighted variance:
- Weighted covariance:
- Weighted correlation:
What the Data Reveals
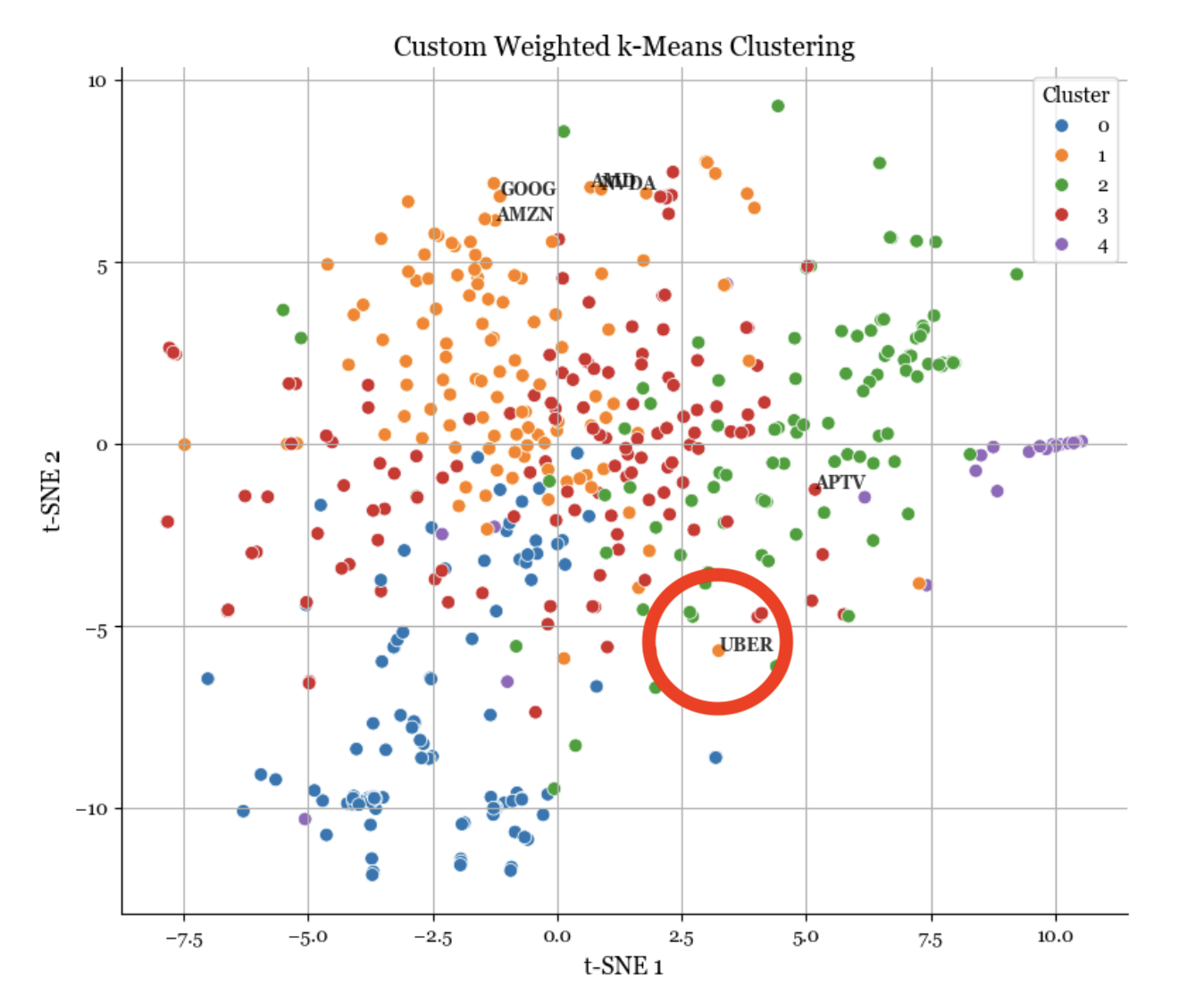
Before diving into the results, let’s summarize the key setup of our experiment. We analyzed daily log returns of all S&P 500 constituents over a 2-year period, from September 2022 to September 2024. The number of clusters was chosen to be 5, based on the elbow method, which provided a good trade-off between granularity and interpretability. Importantly, we used a weighted version of the k-means algorithm, where more recent data points in each time series were given exponentially higher importance. The weights followed a half-life of 6 months, meaning that a return observed 6 months ago has half the influence of today’s return in the clustering procedure. This weighting scheme does not affect the raw return data itself, but rather the way similarity (correlation) is computed and how cluster centroids are updated—allowing the algorithm to adapt more quickly to structural changes in the market. To visualize the clustering results, we use t-SNE, a nonlinear dimensionality reduction technique that projects the high-dimensional data into a low dimension space while preserving local structure, making the clusters easier to interpret than with standard methods like PCA.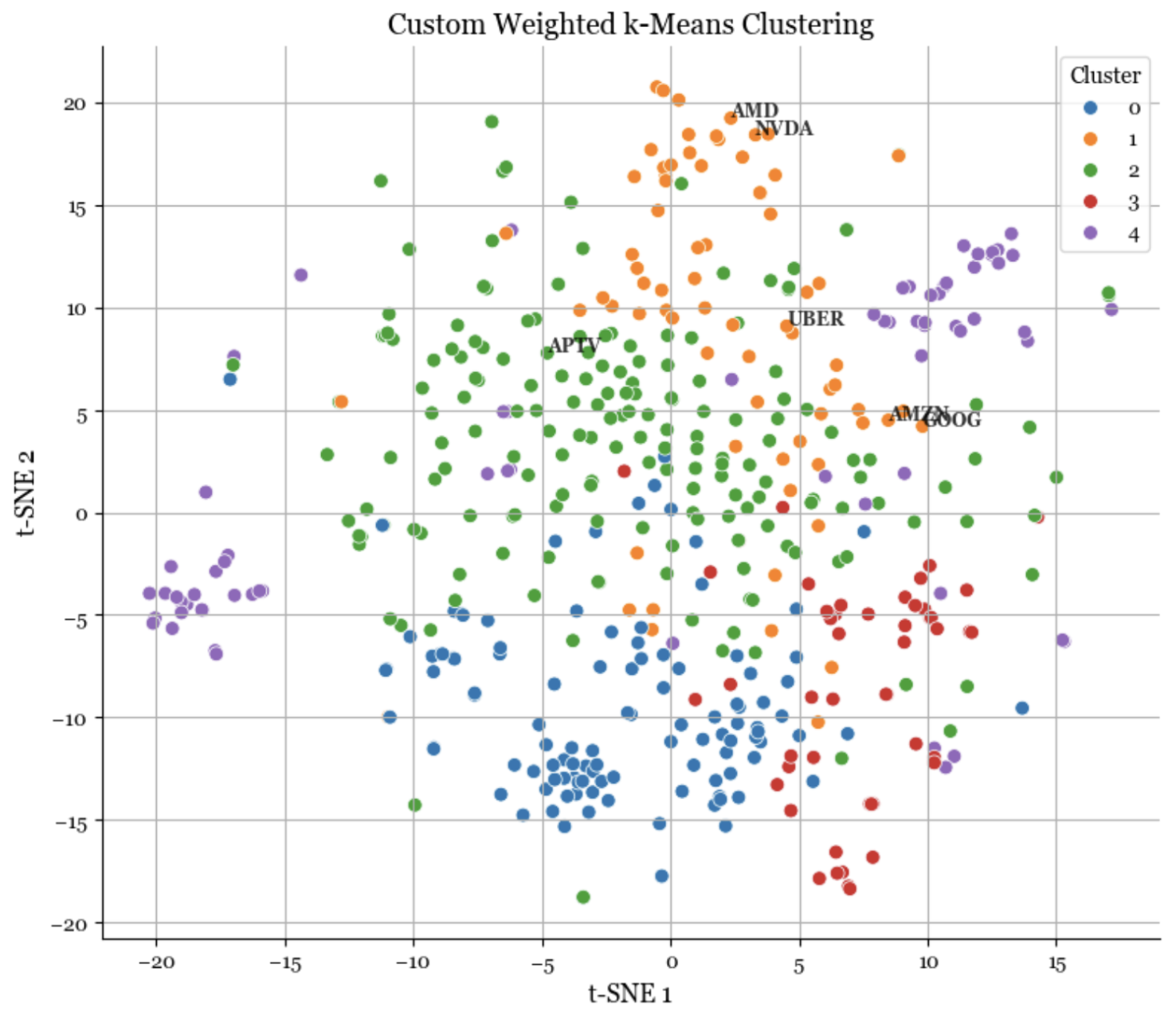
Figure 1: Projection of custom k-means
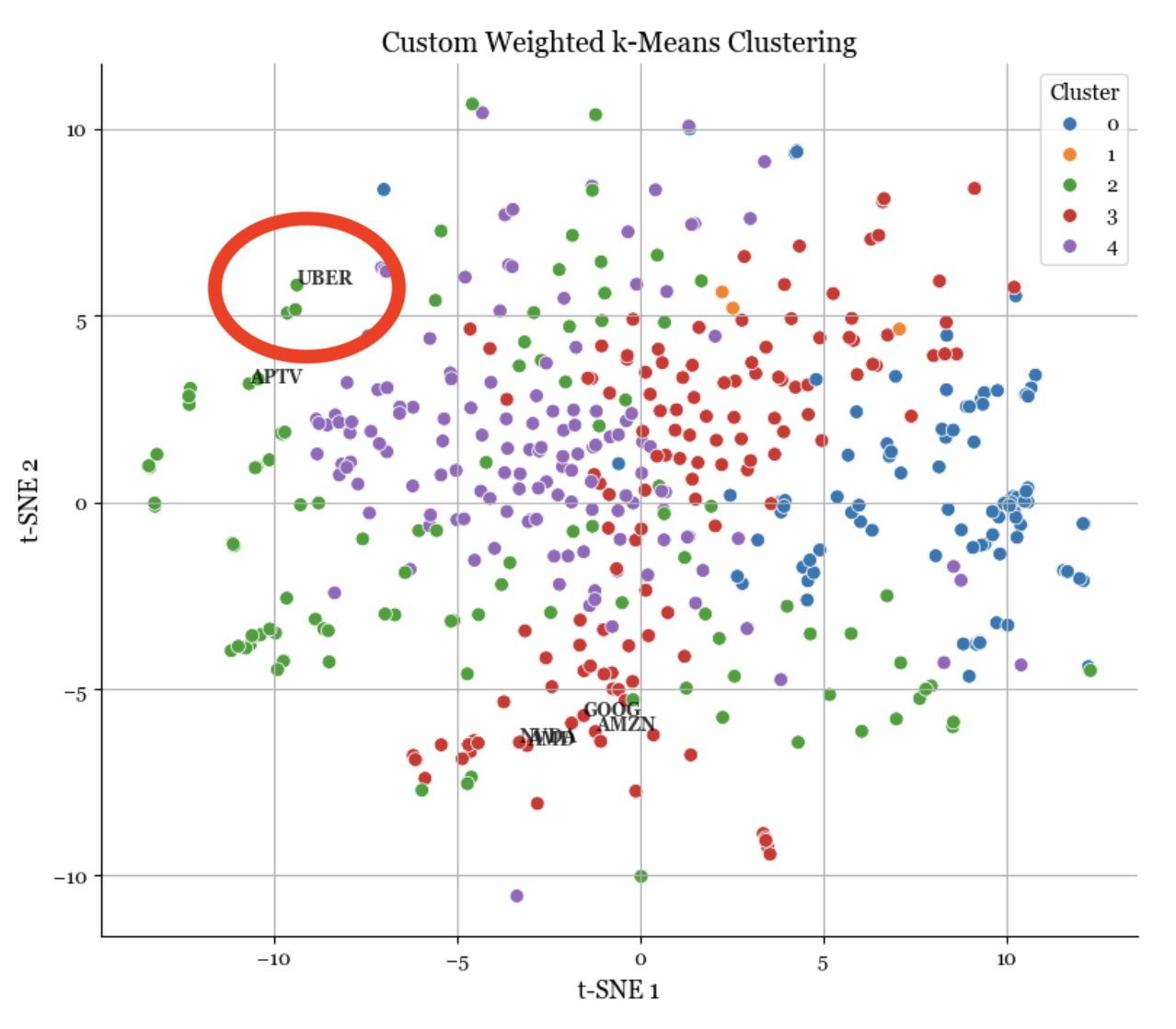
Capturing Structural Shift
To evaluate how well our method captures structural shifts, we ran a comparison around a key moment in recent financial history: the onset of COVID. Specifically, we ran our clustering algorithm using data from a time period ending shortly before COVID was formally recognized by markets, and then again using data that extends just beyond that point. The goal was to see whether our approach could detect changes in how stocks behave as major news unfolds. The results are telling.